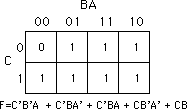

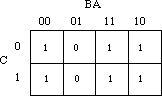
F=C'B'A + C'BA' + C'BA +
CB'A' + CB'A + CBA' + CBA. The figure below shows the truth map for
this function.

Each rectangle represents a term in the simplified boolean function.
Therefore, the simplified boolean function will contain only three terms.
You build each term using the process of elimination. You eliminate any
variables whose primed and unprimed form both appear within the rectangle.
Consider the long skinny rectangle above that is sitting in the row where
C=1. This rectangle contains both A and B in primed and unprimed form. Therefore,
we can eliminate A and B from the term. Since the rectangle sits in the
C=1 region, this rectangle represents the single literal C.
Now consider the solid square above. This rectangle includes C, C', B, B'
and A. Therefore, it represents the single term A. Likewise, the square
with the dotted line above contains C, C', A, A' and B. Therefore, it represents
the single term B.
The final, optimal, function is the sum (logical OR) of the terms represented
by the three squares. Therefore, F= A + B + C. You do not have
to consider squares containing zeros.
When enclosing groups of ones in the truth map, you must consider the fact
that a truth map forms a torus (i.e., a doughnut shape). The right edge
of the map wraps around to the left edge (and vice-versa). Likewise, the
top edge wraps around to the bottom edge. This introduces additional possibilities
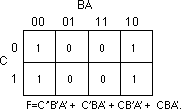
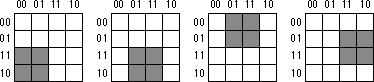
when surrounding groups of ones in a map. Consider the boolean function
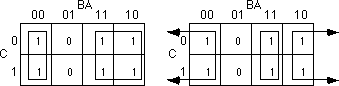
F=C'B'A' + C'BA' + CB'A' + CBA'. The figure below shows the
truth map for this function
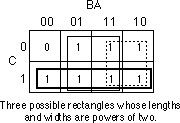
At first glance, you would think that there are two possible rectangles
here as the figure below shows.
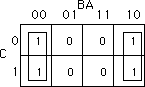
However, because the truth map is a continuous object with the right
side and left sides connected, we can form a single, square rectangle, as
shown below:

So what? Why do we care if we have one rectangle or two in the truth
map? The answer is because the larger the rectangles are, the more terms
they will eliminate. The fewer rectangles that we have, the fewer terms
will appear in the final boolean function. For example, the former example
with two rectangles generates a function with two terms. The first rectangle
(on the left) eliminates the C variable, leaving A'B' as its term. The second
rectangle, on the right, also eliminates the C variable, leaving the term
BA'. Therefore, this truth map would produce the equation F=A'B' + A'B.
We know this is not optimal, see Th 13. Now consider the second truth map
above. Here we have a single rectangle so our boolean function will only
have a single term. Obviously this is more optimal than an equation with
two terms. Since this rectangle includes both C and C' and also B and B',
the only term left is A'. This boolean function, therefore, reduces to F=A'.
There are only two cases that the truth map method cannot handle properly:
a truth map that contains all zeros or a truth map that contains all ones.
These two cases correspond to the boolean functions F=0 and F=1, respectively.
These functions are easy to generate by inspection of the truth map.
An important thing you must keep in mind when optimizing boolean functions
using the mapping method is that you always want to pick the largest rectangles
whose sides' lengths are a power of two. You must do this even for overlapping
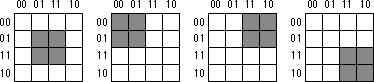
rectangles (unless one rectangle encloses another). Consider the boolean
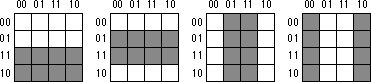
function F = C'B'A' + C'BA' + CB'A' + C'AB + CBA' + CBA. This
produces the truth map appearing below:
The initial temptation is to create one of the sets of rectangles found
below:
However, the correct mapping is

All three mappings will produce a boolean function with two terms. However,
the first two will produce the expressions F= B + A'B' and
F = AB + A'. The third form produces F = B + A'.
Obviously, this last form is more optimal than the other two forms (see
theorems 11 and 12).
For functions of three variables, the size of the rectangle determines the
number of terms it represents:

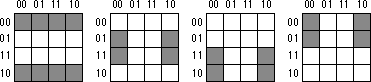
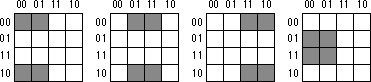
F = D'C'B'A' + D'C'B'A + D'C'BA +
D'C'BA' + D'CB'A + D'CBA + DCB'A + DCBA + DC'B'A' + DC'BA', the truth
map appears below: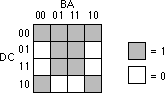
Here are two possible sets of maximal rectangles for this function, each
producing three terms
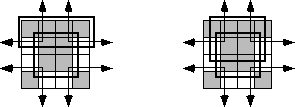
Both functions are equivalent; both are as optimal as you can get. Either
will suffice for our purposes.
First, let's consider the term represented by the rectangle formed by the
four corners. This rectangle contains B, B', D, and D'; so we can eliminate
those terms. The remaining terms contained within these rectangles are C'
and A', so this rectangle represents the term C'A'.
The second rectangle, common to both maps in the figure, is the rectangle
formed by the middle four squares. This rectangle includes the terms A,
B, B', C, D, and D'. Eliminating B, B', D, and D' (since both primed and
unprimed terms exist), we obtain CA as the term for this rectangle.
The map on the left in the figurehas a third term represented by the top
row. This term includes the variables A, A', B, B', C' and D'. Since it
contains A, A', B, and B', we can eliminate these terms. This leaves the
term C'D'. Therefore, the function represented by the map on the left is
F=C'A' + CA + C'D'.
The map on the right in the figure has a third term represented by the top/middle
four squares. This rectangle subsumes the variables A, B, B', C, C', and
D'. We can eliminate B, B', C, and C' since both primed and unprimed versions
appear, this leaves the term AD. Therefore, the function represented by
the function on the right is F=C'A' + CA + AD'.
Since both expressions are equivalent, contain the same number of terms,
and the same number of operators, either form is equivalent. Unless there
is another reason for choosing one over the other, you can use either form.